2021年教师招聘考试《中学数学》考前押题4

试卷预览

1 单选题 1分

已知BD为正方形ABCD对角线，M为BD上不同于B、D的一个动点，以AB为边在ABCD侧边作等边三角形ABE，以BM为边在BD左侧作等边三角形BMF，连接EF、AM、CM，当AM+BM+CM最短时，∠BCM=( )。

查看答案 开始考试

正确答案：A

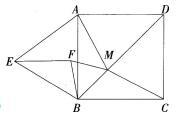
本题解析：

2 单选题 1分

在矩形ABCD中，AB=16cm，AD=6cm，动点P、Q分别从A、C两处出发，点P以3cm/s的速度向点B移动，一直到点曰，点Q以2cm／s向D移动，当P,Q距离为10cm时，P、Q两点从出发开始经过时间为( )s。

查看答案 开始考试

正确答案：C

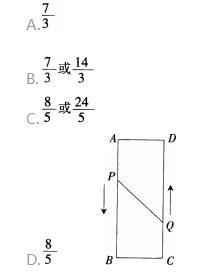
本题解析：

3 单选题 1分

对于求函数f(x)=x3+2x2-x+1，x∈[-1，3]最大值的问题，下列关于该问题的解题过程蕴涵的主要数学思想的表述中，不恰当的一项是( )。

查看答案 开始考试

正确答案：B

本题解析：

求解闭区间上函数最值过程中运用了划归与转化思想、方程与函数思想将问题转化成求函数导数及导函数的零点。还运用了有限与无限思想，在函数极值点和区间端点中找函数的最大值与最小值。

4 单选题 1分

相交两圆的圆心距是5，如果其中一个圆的半径是3，那么另一个圆的半径可以是( )。

查看答案 开始考试

正确答案：B

本题解析：

设两圆的半径分别为r1和r2，圆心距为d，其中r1=3，d=5，则存在以r1,r2，d为三边的三角形。即满足d-r1

5 单选题 1分

查看答案 开始考试

正确答案：D

本题解析：

6 单选题 1分

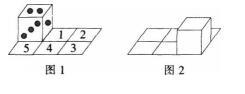
在二行三列的方格棋盘上沿骰子的某一条棱翻滚(向对面分别为1和6，2和5，3和4)。在每一种翻动方式中，骰子不能后退，开始如图1所示，2朝上，最后到图2形式，此时向上的点数不可能是( )。

查看答案 开始考试

正确答案：D

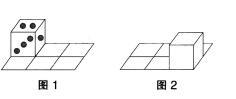
本题解析：

如图所示，第一种路径：滚动到位置1处，1在下，则6在上；滚动到位置2处，2在下，5在上；滚动到3处，3在下，则4在上；第二种路径：滚动到位置1处，1在下，则6在上；滚动到4处，3在下，4在上；滚动到3处，2在下，5在上；第三种路径：滚动到5处，3在下，4在上；滚动到4处，1在下，6在上，滚动到3 处，4在下，3在上；所以最后朝上的可能性有3，4，5，而不会出现1，2。故选D。

7 单选题 1分

设函数f(x)在[a，b]上连续，则f(a) f(b)<0是方程f(x)=0在(a，b)上至少有一根的( )。

查看答案 开始考试

正确答案：A

本题解析：

根据零点存在定理，函数f(x)在[a，b]上连续，且f(a)*f(b)<0，∴函数在区间(a，b)上至少有一个零点。 ∴方程f(x)=0在(a，b)上至少有一个实根。反之则不然。因此是充分不必要条件。

8 单选题 1分

一个袋中装有形状大小完全相同，编号分别为1，2，3，4，5，6的六个球，现从口袋中任取两个球，则至少取到一个编号为质数的球的概率是( )。

查看答案 开始考试

正确答案：B

本题解析：

9 单选题 1分

查看答案 开始考试

正确答案：A

本题解析：

10 单选题 1分

查看答案 开始考试

正确答案：D

本题解析：