2020年1220江苏省公务员考试《行测》真题（A类）

试卷预览

1 单选题 1分

2019年全球太空经济规模增至3660亿美元，较2018年增长1.7%，其中全球卫星产业收入为2707亿美元。在全球卫星产业收入中，卫星制造业的收入为125亿美元，较上年减少70亿美元；卫星发射服务业的收入为49亿美元，较上年下降21.0%；卫星通信服务业的收入为1230亿美元，较上年减少35亿美元；地面设备制造业的收入为1303亿美元，较上年增长4.1%。

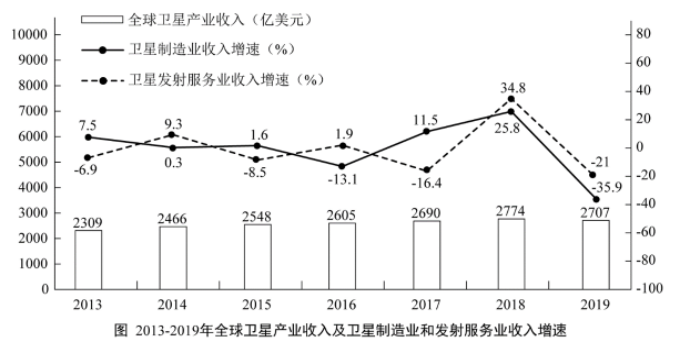
关于2019年全球卫星产业，能够从上述资料中推出的是：

查看答案 开始考试

正确答案：A

本题解析：

第一步，本题考查综合分析问题，且需选出正确的一项。

第二步，A选项，增长率计算。定位图形材料，“全球卫星产业收入2018年为2774亿美元，2019年为2707亿美元”，根据增长率，代入数据可得2019年全球卫星产业收入增速为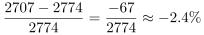，正确。

B选项，间隔增长率计算。定位图形材料，“卫生发射服务业收入2018年同比增速为34.8%，2019年同比增速为－21.0%”，根据间隔增长率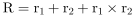，代入数据可得2019年卫生发射服务业收入比2017年提高了34.8%－21.0%＋34.8%×（－21.0%）=13.8%－34.8%×21.0%＜13.8%，提高了不到13.8个百分点，错误。

C选项，两期比重比较。定位文字材料，“2019年全球太空经济规模增至3660亿美元，较2018年增长1.7%”，根据两期比重比较口诀，部分增速高于整体增速，比重上升，反之则下降，由本题A选项可知2019年卫星产业收入同比增速a（－2.4%）＜b（1.7%），比重下降，错误。

D选项，增长量计算。定位文字材料，“卫星通信服务业的收入为1230亿美元，较上年减少35亿美元；地面设备制造业的收入为1303亿美元，较上年增长4.1%”，4.1%≈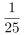，根据增长量计算n＋1原则，可得地面设备制造业收入的同比增量为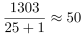（亿美元），卫星通信服务业收入的同比增量为－35亿美元，增长量相差50－（－35）=85（亿美元），错误。

因此，选择A选项。

2 单选题 1分

2019年全球太空经济规模增至3660亿美元，较2018年增长1.7%，其中全球卫星产业收入为2707亿美元。在全球卫星产业收入中，卫星制造业的收入为125亿美元，较上年减少70亿美元；卫星发射服务业的收入为49亿美元，较上年下降21.0%；卫星通信服务业的收入为1230亿美元，较上年减少35亿美元；地面设备制造业的收入为1303亿美元，较上年增长4.1%。

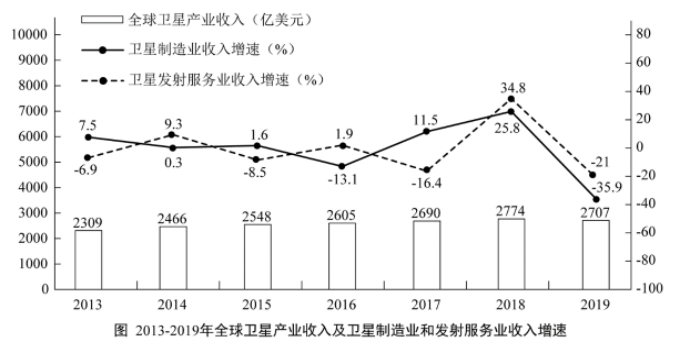
2014—2019年全球卫星产业收入增速大于卫星发射服务业的年份数有：

查看答案 开始考试

正确答案：C

本题解析：

第一步，本题考查增长率计算比较。

第二步，定位图形材料，“2014—2019年全球卫星发射服务业的同比增速分别为9.3%、－8.5%、1.9%、－16.4%、34.8%、－21.0%”。

第三步，根据增长率，将数据截位舍相同处理，代入数据可得全球卫星产业收入增速分别为：2014年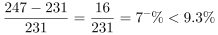，；2015年实现正增长，增长率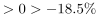；2016年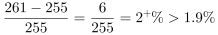，；2017年实现正增长，增长率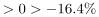；2018年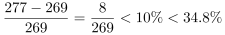，；2019年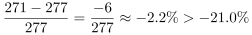，，2014—2019年全球卫星产业收入增速大于卫星发射服务业的有2015年、2016年、2017年和2019年，共4年。

因此，选择C选项。

3 单选题 1分

2019年全球太空经济规模增至3660亿美元，较2018年增长1.7%，其中全球卫星产业收入为2707亿美元。在全球卫星产业收入中，卫星制造业的收入为125亿美元，较上年减少70亿美元；卫星发射服务业的收入为49亿美元，较上年下降21.0%；卫星通信服务业的收入为1230亿美元，较上年减少35亿美元；地面设备制造业的收入为1303亿美元，较上年增长4.1%。

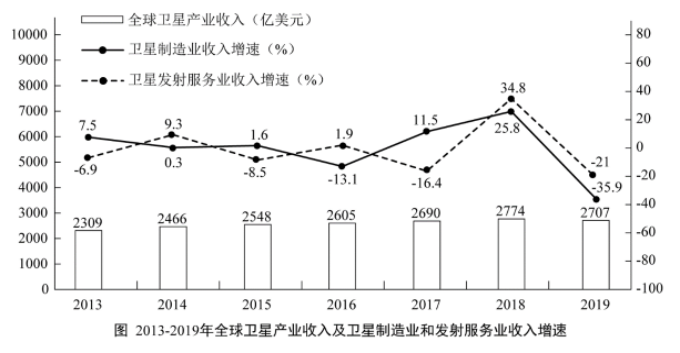
以2012年为基期，2019年全球卫星制造业、卫星发射服务业的收入增长情况分别是：

查看答案 开始考试

正确答案：B

本题解析：

第一步，本题考查增长率计算。

第二步，定位图形材料中的折线图。

第三步，根据现期量=基期量×（1+r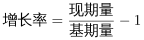）、，可得2019年全球卫星制造业收入=2012年全球卫星制造业收入×（1+7.5%）×（1+0.3%）×（1+1.6%）×（1-13.1%）×（1+11.5%）×（1+25.8%）×（1-35.9%），则全球卫星制造业收入2019年比2012年的增长率为（1+7.5%）×（1+0.3%）×（1+1.6%）×（1-13.1%）×（1+11.5%）×（1+25.8%）（1－35.9%）-1=1.075×1.003×1.016×0.869×1.115×1.258×0.641－1=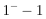＜0，增长率小于0，为负增长。

2019年卫星发射服务业收入=2012年卫星发射服务业收入×（1-6.9%）×（1+9.3%）×（1-8.5%）×（1+1.9%）×（1-16.4%）×（1+34.8%）×（1－21%），则卫星发射服务业收入2019年比2012年的增长率为（1-6.9%）×（1+9.3%）×（1-8.5%）×（1+1.9%）×（1-16.4%）×（1+34.8%）（1－21%）-1=0.931×1.093×0.915×1.019×0.836×1.348×0.79-1=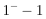＜0，增长率小于0，为负增长。

因此，选择B选项。

4 单选题 1分

2019年全球太空经济规模增至3660亿美元，较2018年增长1.7%，其中全球卫星产业收入为2707亿美元。在全球卫星产业收入中，卫星制造业的收入为125亿美元，较上年减少70亿美元；卫星发射服务业的收入为49亿美元，较上年下降21.0%；卫星通信服务业的收入为1230亿美元，较上年减少35亿美元；地面设备制造业的收入为1303亿美元，较上年增长4.1%。

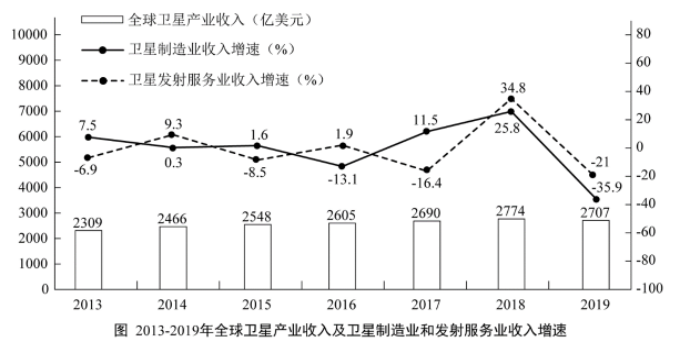
2014—2019年全球卫星产业收入增长最快的年份是：

查看答案 开始考试

正确答案：A

本题解析：

第一步，本题考查增长率计算比较。

第二步，定位图形材料中的柱状图。

第三步，根据增长率=（现期量-基期量）/基期量，各年份增长率分别为：2014年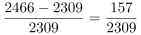，；2015年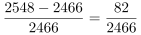，；2017年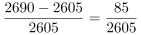，；2018年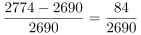，，根据分数性质，分子大分母小，分数值大，2014年分子最大，分母最小，分数值最大，则增速最大的为2014年。

因此，选择A选项。

5 单选题 1分

2019年全球太空经济规模增至3660亿美元，较2018年增长1.7%，其中全球卫星产业收入为2707亿美元。在全球卫星产业收入中，卫星制造业的收入为125亿美元，较上年减少70亿美元；卫星发射服务业的收入为49亿美元，较上年下降21.0%；卫星通信服务业的收入为1230亿美元，较上年减少35亿美元；地面设备制造业的收入为1303亿美元，较上年增长4.1%。

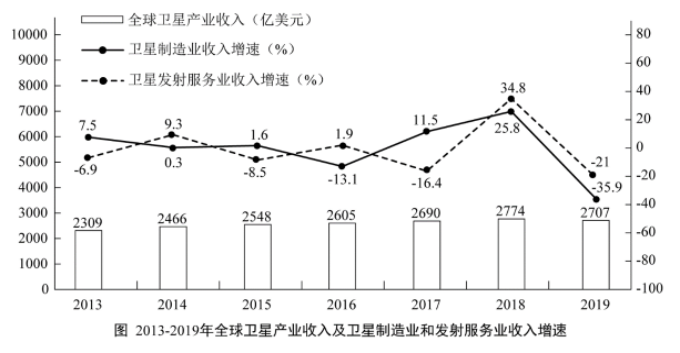
2019年全球卫星制造业收入占卫星产业收入的比重为：

查看答案 开始考试

正确答案：D

本题解析：

第一步，本题考查现期比重计算中的求比重。

第二步，定位文字材料，“（2019年）全球卫星产业收入为2707亿美元。在全球卫星产业收入中，卫星制造业的收入为125亿美元”。

第三步，根据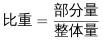，选项首位不同，分母从左向右截取前两位，可得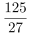，直除首位商4。

因此，选择D选项。

6 单选题 1分

国家统计局采用定基指数方法，以2014年为100，根据第四次全国经济普查数据修订结果以及部分指标最新数据，将5个分类指标的权重均设定为0.2，对2015—2019年我国经济发展新动能总指数进行测算，结果见下表。

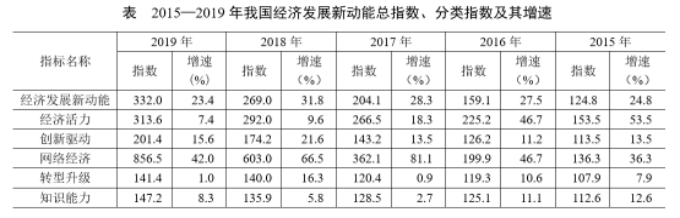
注：分类指数对总指数增长的贡献率计算公式为

能够从上述资料中推出的是：

查看答案 开始考试

正确答案：C

本题解析：

第一步，本题考查综合分析，且需选出正确的一项。

第二步，A选项，年均增长量计算。定位表格材料，根据年均增长量=，江苏省考中年均增长量类计算需要“翻旧账”，即初期为2015年末，即2014年末的数据（100），将数据做取整处理，可得2015—2019年我国创新驱动指数年均增量约为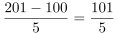=20.2＜40.3，错误。

B选项，增长贡献率比较。定位表格材料，根据增长贡献率=，分类指数权重一致，可知比较2016年和2015年我国知识能力指数对总指数增长的贡献率，只需比较即可，2016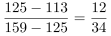年2015年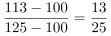，即2016年，我国知识能力指数对总指数增长的贡献率低于2015年，错误。

C选项，年均增长率计算。定位表格材料，根据年均增长率计算公式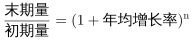，，江苏省考中年均增长率需要“翻旧账”，即初期为2015年初，即2014年末（指数为100），代入数据可得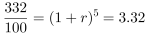，当年均增长率为25%时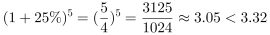，，则年均增速应＞25%，正确。

D选项，读数比较。定位表格材料，直接读数可知，2018年转型升级的增速为16.3%＞知识能力的增速5.8%，不是最慢，错误。

因此，选择C选项。

7 单选题 1分

国家统计局采用定基指数方法，以2014年为100，根据第四次全国经济普查数据修订结果以及部分指标最新数据，将5个分类指标的权重均设定为0.2，对2015—2019年我国经济发展新动能总指数进行测算，结果见下表。

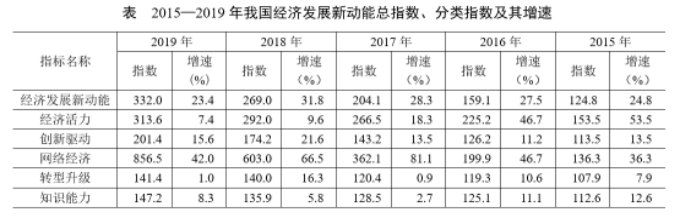
注：分类指数对总指数增长的贡献率计算公式为

2016—2018年指数值累计增量最多和最少的分类指数分别是：

查看答案 开始考试

正确答案：A

本题解析：

第一步，本题考查增长量比较问题。

第二步，定位表格材料。

第三步，2016—2018年指数值累计增量即为时间段内的总增量，江苏省考中时间段内求总增量需要“翻旧账”，初期为2016年初，即2015年末，故总增量=2018年指数值－2015年指数值。

第四步，将数据简单取整可得，网络经济指数的总增量为603－136=467＞经济活力指数的总增量为292－154=138，故最多的为网络经济指数，排除B、D选项；知识能力指数的总增量为136－113=23＜转型升级指数的总增量为140－108=32，故总增量最少的为知识能力指数，排除C选项。

因此，选择A选项。

8 单选题 1分

国家统计局采用定基指数方法，以2014年为100，根据第四次全国经济普查数据修订结果以及部分指标最新数据，将5个分类指标的权重均设定为0.2，对2015—2019年我国经济发展新动能总指数进行测算，结果见下表。

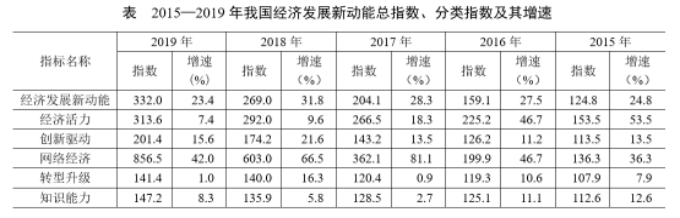
注：分类指数对总指数增长的贡献率计算公式为

在5个分类指数中，2019年对总指数增长的贡献率大于2018年的有：

查看答案 开始考试

正确答案：B

本题解析：

第一步，本题考查增长贡献率比较问题。

第二步，定位表格材料和文字材料“将5个分类指数的权重均设定为0.2”。

第三步，根据增长贡献率

9 单选题 1分

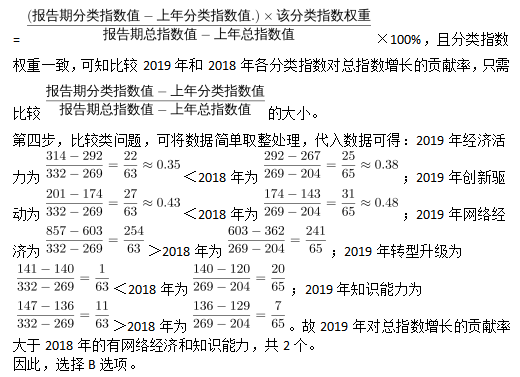
国家统计局采用定基指数方法，以2014年为100，根据第四次全国经济普查数据修订结果以及部分指标最新数据，将5个分类指标的权重均设定为0.2，对2015—2019年我国经济发展新动能总指数进行测算，结果见下表。

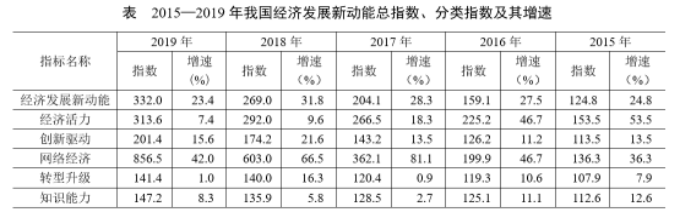
注：分类指数对总指数增长的贡献率计算公式为

2015—2019年我国经济发展新动能总指数值比上年增加最多的年份是：

查看答案 开始考试

正确答案：C

本题解析：

第一步，本题考查增长量计算问题。

第二步，定位表格“经济发展新动能15年至19年的指数数据”。

第三步，根据增长量=现期量－基期量，比较类问题，可将数据简单取整处理，代入数据可得2016年的增长量为159－125=34，2017年的增长量为204－159=45，2018年的增长量为269－204=65，2019年的增长量为332－269=63，则同比增加最多的是2018年。

因此，选择C选项。

10 单选题 1分

国家统计局采用定基指数方法，以2014年为100，根据第四次全国经济普查数据修订结果以及部分指标最新数据，将5个分类指标的权重均设定为0.2，对2015—2019年我国经济发展新动能总指数进行测算，结果见下表。

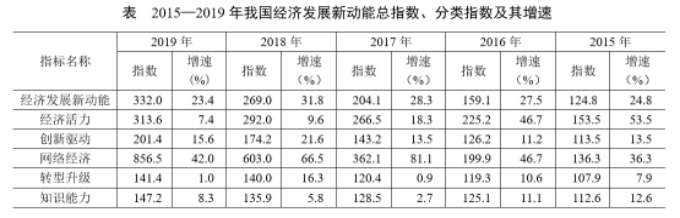
注：分类指数对总指数增长的贡献率计算公式为

2019年我国网络经济指数对总指数增长的贡献率为：

查看答案 开始考试

正确答案：D

本题解析：

第一步，本题考查增长贡献率计算问题。

第二步，定位标注中的贡献率公式和表格数据可知，“2019年网络经济报告期指数为856.5、2018年为603.0；2019年报告期总指数332.0、2018年为269.0”，定位文字材料可知，“5个分类指数的权重均为0.2”。

第三步，根据增长贡献率=×100%，选项首位相同第二位不同，则分母从左向右截取前三位，分子和分母均为减法，考虑截位舍相同处理数据，代入数据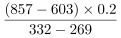，×100%=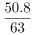，直除首位商8。

因此，选择D选项。