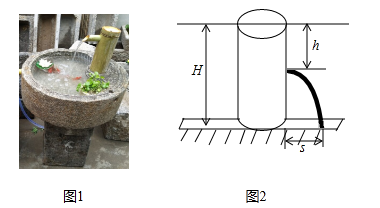
24.用各种盛水容器可以制作精致的家用流水景观(如图1).
科学原理:如图2,始终盛满水的圆体水桶水面离地面的高度为H(单位:cm),如果在离水面竖直距离为h(单位:cm)的地方开大小合适的小孔,那么从小孔射出水的射程(水流落地点离小孔的水平距离)s(单位:cm)与h的关系为s2=4h(H﹣h).
应用思考:现用高度为20cm的圆柱体望料水瓶做相关研究,水瓶直立地面,通过连注水保证它始终盛满水,在离水面竖直距高hcm处开一个小孔.
(1)写出s2与h的关系式;并求出当h为何值时,射程s有最大值,最大射程是多少?
(2)在侧面开两个小孔,这两个小孔离水面的竖直距离分别为a,b,要使两孔射出水的射程相同,求a,b之间的关系式;
(3)如果想通过垫高塑料水瓶,使射出水的最大射程增加16cm,求整高的高度及小孔离水面的竖直距离.