当前位置：首页 → 学历类 → 高考 → 数学（文科）->2022年山西省高考文科数学押题试卷

2022年山西省高考文科数学押题试卷

卷面总分：23分 答题时间：240分钟 试卷题量：23题 练习次数：124次
单选题 （共12题，共12分）
1.

集合 M＝{x∈R|0＜x≤2022}， N＝{x|x＝2k， k∈Z}， 则 M∩ N 所含元素个数为（）

  • A. 2022
  • B. 2023
  • C. 3
  • D. 1011
标记 纠错
2.

image.png

  • A. A
  • B. B
  • C. C
  • D. D
标记 纠错
3.

设样本数据 1， 2， x， 4， 5 的均值等于 4， 则数据 5， 11， 7， x， 10， 6， 9 的标准差等于（）

  • A. 1
  • B. 2
  • C. 3
  • D. 4
标记 纠错
4.

image.png

  • A. A
  • B. B
  • C. C
  • D. D
标记 纠错
5.

image.png

  • A. A
  • B. B
  • C. C
  • D. D
标记 纠错
6.

image.png

  • A. 圆
  • B. 椭圆
  • C. 抛物线
  • D. 直线
标记 纠错
7.

在△ABC 中， AB= √2， BC= √3， CA＝2， 则△ABC 外接圆的面积为（）

image.png

  • A. A
  • B. B
  • C. C
  • D. D
标记 纠错
8.

已知直线 l 1 ， l 2 ， l 1 ⊥l 2 于点 H， A∈l 1 且|AH|＝36， B∈l 2 ， 点 M 在线段 AB 的垂直平分线上且 MB⊥l 2 ， 则|MA|的最小值为（）

  • A. 9
  • B. 18
  • C. 36
  • D. 72
标记 纠错
9.

我们非常熟悉： “直角三角形的两直角边的平方和等于斜边的平方”， 这个规律在中国被称为勾股定理， 勾股定理是几何学中一颗璀璨夺目的明珠， 被称为“几何学的基石”， 而且在高等数学和其他学科中也有着极为广泛的应用． 世界上的几个文明古国都发现过此定理并且进行了广泛深入的研究， 因此有许多名称， 譬如古希腊毕达哥拉斯发现研究过此定理， 又称为毕达哥拉斯定理． 中国是发现和研究勾股定理最古老的国家之一， 中国古代数学家称直角三角形为勾股形， 较短的直角边称为勾， 另一直角边称为股， 斜边称为弦， 所以勾股定理也称为勾股弦定理． 如果一个勾股形的“勾”“股”“弦” 都是整数，其中“勾” 等于 11， 那么这个勾股形的周长等于（）

  • A. 40
  • B. 84
  • C. 90
  • D. 132
标记 纠错
10.

已知某几何体的三视图如图所示， 则该几何体的内切球的半径等于（）

image.png

  • A. A
  • B. B
  • C. C
  • D. D
标记 纠错
11.

image.png

  • A. a＜c＜b
  • B. a＜b＜c
  • C. b＜a＜c
  • D. c＜b＜a
标记 纠错
12.

image.png

则正确命题的序号是（）

  • A. ③④
  • B. ①③④
  • C. ②③④
  • D. ①③
标记 纠错
填空题 （共4题，共4分）
13.

image.png

标记 纠错
14.

image.png

标记 纠错
15.

image.png

标记 纠错
16.

有一个空心球体， 其外表球面外接于底面半径等于 1、 母线长等于 3 的圆锥， 空心球体的内壁面是球面， 且内壁面内切于上述圆锥， 则这个空心球体的体积等于

标记 纠错
问答题 （共7题，共7分）
17.

image.png

image.png

标记 纠错
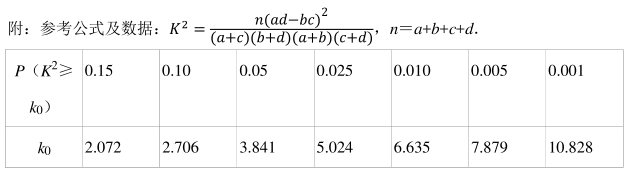
18.

某学校高三理科实验班共计 40 名学生， 在备考复习教学中进行了 8 次规范性的考试， 将每个学生 8 次考试的数学平均分、 物理平均分制成茎叶图如下． 数学满分 150分， 达到或超过 120 分认为是良好的； 物理满分 120 分， 成绩达到或超过 96 分认为是良好的． 已知数学良好的学生中， 恰好有 4 人物理不良好

image.png

（1） 求数学成绩的众数、 中位数；

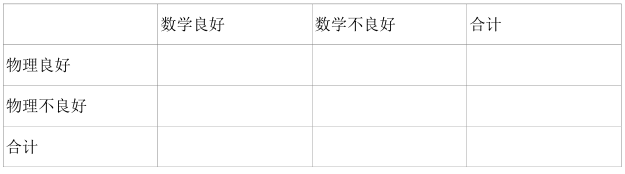
（2） 请填写下面列联表， 并根据列联表判断是否有 99.5%的把握认为学生物理良好与数学良好有关？

image.png

（3） 在物理不良好的学生中按照数学是否良好分层抽取 5 位同学， 再从这 5 位同学中抽取两位进行数学基础是否对物理学习有影响的深度访谈， 求被抽到的两位同学恰好有一位数学良好的概率．

image.png

标记 纠错
19.

如图， 在四棱锥 P﹣ ABCD 中， ABCD 是菱形， E， F分别是△PAD， △PAB 的重心， 平面 PCD⊥平面 ABCD， 平面 PBC⊥平面 ABCD．

（1） 求证： EF∥平面 ABCD；

（2） 求证； 平面 PEF⊥平面 PAC．

image.png

标记 纠错
20.

image.png

image.png

标记 纠错
21.

image.png

image.png

标记 纠错
22.

image.png

image.png

标记 纠错
23.

 已知函数 f（x） ＝2|x﹣ 1|﹣ |x+1|．

（1） 在答题卡所给出的网格坐标系中作出函数 f（x） 的图象（不要求写作法）， 并直接写出函数 f（x） 的最小值；

（2） 已知函数 g（x） ＝|x+a|﹣ 2|x﹣ a|， 若存在 x 1 ， x 2 ∈R 使 f（x 1 ） +5＝g（x 2 ）， 求实数a 的取值范围．

image.png

标记 纠错

答题卡（剩余 道题）

单选题
1 2 3 4 5 6 7 8 9 10 11 12
填空题
13 14 15 16
问答题
17 18 19 20 21 22 23
00:00:00
暂停
交卷
友情链接

答案圈武汉生活网吾爱诗经网

Copyright © 2018-2022 http://tk.mxqe.com/ Corporation, All Right Reserved 客服联系：2645034912@qq.com  备案号：鄂ICP备17009702号-1