推荐等级：
发布时间： 2022-12-09 08:38
扫码用手机做题
2021年，全国移动通信基站总数达996万个，全年净增65万个。其中4G基站达590万个，5G基站为142.5万个，全年新建5G基站约65万个。
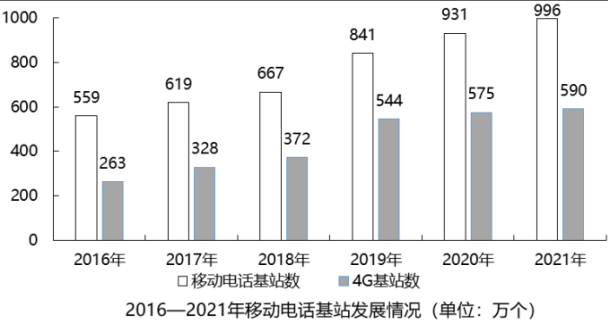
根据上述材料，以下说法不正确的是：
本题解析：
第一步，本题考查综合分析问题，且需选出错误的一项。
第二步，A选项，增长率计算。定位文字材料，根据增长率=
，代入数据可得
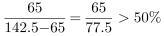，错误。
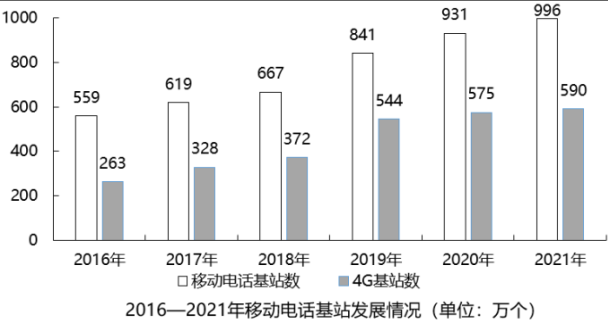
B选项，增长量做差比较。定位图形材料，根据增长量=现期量－基期量，显然2019年同比增量841－667＞100（万个），其余年份增量均不到100万个，正确。
C选项，简单计算中的和差比较。定位图形材料，显然2021年除4G以外的基站数996－590＞400（万个），其余年份均不到400万个，正确。
D选项，年均增长率比较。定位图形材料，根据
，相差年数n相同，比较年均增速的大小，只需比较
，全国移动通信基站总数
＜4G基站
，则年均增速低于4G基站，正确。
因此，选择A选项。
2021年，全国移动通信基站总数达996万个，全年净增65万个。其中4G基站达590万个，5G基站为142.5万个，全年新建5G基站约65万个。
2016—2021年，全国移动通信基站总数中，4G基站数占比最高的是：
本题解析：
第一步，本题考查比重比较。
第二步，定位图形材料。
第三步，根据比重=
，代入数据可得各年比重分别为：2018年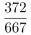
，2019年
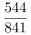，2020年
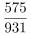，2021年
，直除首位分别商5，6，6，5，排除A、D选项；2019年和2020年直除首两位分别商64，61，则占比最高的是2019年。
因此，选择B选项。
2021年，全国移动通信基站总数达996万个，全年净增65万个。其中4G基站达590万个，5G基站为142.5万个，全年新建5G基站约65万个。
若保持2021年4G基站和5G基站各自的增量不变，则（ ）年5G基站数量将超过4G基站数量。
本题解析：
第一步，本题考查现期量计算。
第二步，定位文字材料和图形材料。
第三步，根据末期量=初期量＋n×年均增量，2021年4G基站数的增量为590－575=15（万个），假设n年后5G基站数量将超过4G基站数量，可得142.5＋65n＞590＋15n，解得n=8.95，即至少需要9年，5G基站数量才能超过4G基站数量，2021＋9=2030，即2030年。
因此，选择B选项。
2021年，全国移动通信基站总数达996万个，全年净增65万个。其中4G基站达590万个，5G基站为142.5万个，全年新建5G基站约65万个。
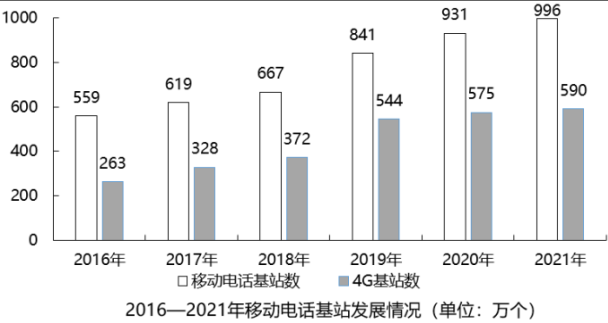
2017—2021年，全国移动通信4G基站数同比增长最快的是：
本题解析：
第一步，本题考查增长率计算比较。
第二步，定位图形材料。
第三步，根据增长率=
，代入数据可得同比增速分别为：2017年
，2018年
，2019年
，2020年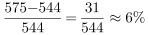
，同比增速最大的是2019年。
因此，选择C选项。
2021年，全国移动通信基站总数达996万个，全年净增65万个。其中4G基站达590万个，5G基站为142.5万个，全年新建5G基站约65万个。
2017—2021年，全国移动电话基站数平均每年约增长（ ）万个。
本题解析：
第一步，本题考查年均增长量计算。
第二步，定位图形材料。
第三步，根据年均增长量=
，初期为2017年，末期为2021年，相差年数为4，代入数据可得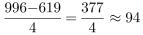
（万个）。
因此，选择C选项。
根据所给材料，回答下列题目。
?某小学春季召开运动会，需要在操场按照从前往后的顺序安排一至七年级的位置，负责运动会的老师在商议后，具体的位置有如下安排：
（1）五年级排在三年级之前；
（2）一年级和三年级中间隔着3个年级；
（3）六年级在二年级之后，中间隔着2个年级；
（4）四年级紧挨着一年级前一位或者后一位。
如果七年级排在第1位，则以下哪项是可能的？
本题解析：
第一步，确定题型。
题干具有匹配特征，确定为分析推理。
第二步，分析条件，进行推理。
本题条件为“七年级排在第1位”，那么还剩下6个位置；
根据条件（2）“一年级和三年级中间隔着3个年级”，存在着四种可能性，如下图：
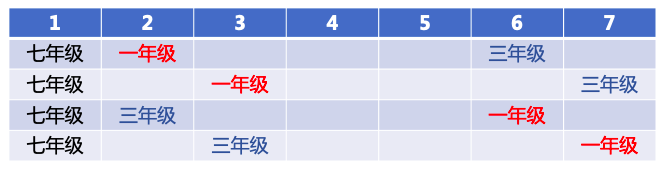
根据条件（1）“五年级排在三年级之前”，故上述可能性变为三种，如下图：
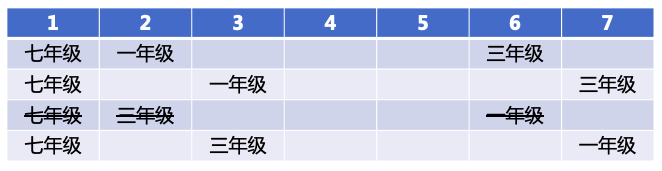
根据条件（3）“六年级在二年级之后，中间隔着2个年级”，故上述可能性变为二种，如下图：
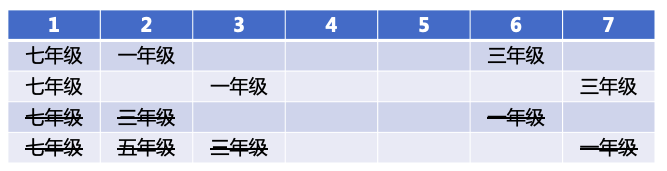
再根据条件（3）“六年级在二年级之后，中间隔着2个年级”，可知两种可能性如下图：
据此辨析选项，只有B项正确。
因此，选择B选项。
根据所给材料，回答下列题目。
?某小学春季召开运动会，需要在操场按照从前往后的顺序安排一至七年级的位置，负责运动会的老师在商议后，具体的位置有如下安排：
（1）五年级排在三年级之前；
（2）一年级和三年级中间隔着3个年级；
（3）六年级在二年级之后，中间隔着2个年级；
（4）四年级紧挨着一年级前一位或者后一位。
如果二年级排在第1位，那么下列哪项中的两年级不可能相邻？
本题解析：
第一步，确定题型。
题干具有匹配特征，确定为分析推理。
第二步，分析条件，进行推理。
本题条件为“二年级排在第1位”，根据条件（3）“六年级在二年级之后，中间隔着2排”，那么六年级在第4排；
利用代入法解题：
代入A项：四年级和五年级相邻
根据条件（4）“四年级紧挨着一年级前一位或者后一位”，可知，“四年级、五年级、一年级”紧挨在一起，那么只能占据5、6、7的位置，但是剩下的2、3是七年级或三年级，但是这与条件（1）“五年级排在三年级之前”冲突，故该项不成立，即四年级和五年级不能相邻；
代入B项：二年级和四年级相邻。
结合条件，存在可能的排序“二年级+四年级+一年级+六年级+七年级+五年级+三年级”，故该项可能，排除；
代入C项：一年级和六年级相邻。
结合条件，存在可能的排序“二年级+四年级+一年级+六年级+七年级+五年级+三年级”，故该项可能，排除；
代入D项：二年级和一年级相邻。
结合条件，存在可能的排序“二年级+一年级+四年级+六年级+五年级+三年级+七年级”，故该项可能，排除。
因此，选择A选项。
根据所给材料，回答下列题目。
?某小学春季召开运动会，需要在操场按照从前往后的顺序安排一至七年级的位置，负责运动会的老师在商议后，具体的位置有如下安排：
（1）五年级排在三年级之前；
（2）一年级和三年级中间隔着3个年级；
（3）六年级在二年级之后，中间隔着2个年级；
（4）四年级紧挨着一年级前一位或者后一位。
二年级和一年级中间最多可能隔几个年级？
本题解析：
第一步，确定题型。
题干具有匹配特征，确定为分析推理。
第二步，分析条件，进行推理。
本题利用代入法验证，由于本题问“最多隔几个年级”，故优先代入D项。
代入D项：即二年级和一年级中间隔5个年级，那么二者在第一位、第七位。
根据条件（3）“六年级在二年级之后，中间隔着2个年级”，所以二年级不能在第7位，只能在第1位，如下：
“二年级、X、X、六年级、X、X、一年级”；
再结合条件（2）“一年级和三年级中间隔着3个年级”，故三年级在第3位，如下：
“二年级、X、三年级、六年级、X、X、一年级”
在结合条件（1）“五年级排在三年级之前”，故五年级在第2位，如下：
“二年级、五年级、三年级、六年级、X、X、一年级”
在结合条件（4）“四年级紧挨着一年级前一位或者后一位”，可知四年级只能在第6位，如下：
“二年级、五年级、三年级、六年级、X、四年级、一年级”
那么剩下的七年级，在第5位，如下：
“二年级、五年级、三年级、六年级、七年级、四年级、一年级”
经验证，代入D项后，与各条件不冲突，本题问“最多隔几个年级”，其他选项无需代入。
因此，选择D选项。
根据所给材料，回答下列题目。
?某小学春季召开运动会，需要在操场按照从前往后的顺序安排一至七年级的位置，负责运动会的老师在商议后，具体的位置有如下安排：
（1）五年级排在三年级之前；
（2）一年级和三年级中间隔着3个年级；
（3）六年级在二年级之后，中间隔着2个年级；
（4）四年级紧挨着一年级前一位或者后一位。
按照从前往后，下列哪项排列是可能的？
本题解析：
第一步，确定题型。
题干具有匹配特征，确定为分析推理。
第二步，分析条件，进行推理。
根据条件（1）“五年级排在三年级之前”，排除B项；
根据条件（3）“六年级在二年级之后，中间隔着2个年级”，排除A项、D项。
因此，选择C选项。
试卷分类：行政职业能力测验
练习次数：93次
试卷分类：行政职业能力测验
练习次数：101次
试卷分类：行政职业能力测验
练习次数：88次
试卷分类：行政职业能力测验
练习次数：158次
试卷分类：行政职业能力测验
练习次数：131次
试卷分类：行政职业能力测验
练习次数：143次
试卷分类：行政职业能力测验
练习次数：118次
试卷分类：行政职业能力测验
练习次数：129次
试卷分类：行政职业能力测验
练习次数：134次
试卷分类：行政职业能力测验
练习次数：122次
